 |
|
Components of the
bullet's flight (path) |
 |
|
Drop |
There is a lot of misleading information and myth flying around ("bull-istics") on the subject of the external ballistics. The tables below will hopefully shed some light on how that bullet really travels once you've pulled the trigger. All tables are rounded to the nearest 10 feet per second and drops are rounded to two places, unless I am trying to show small increments. Greater precision is meaningless in the "real" world. Even for the best of marksman a 1/2 minute of angle difference is effectively meaningless at realistic ranges. The majority of information is presented on rifle cartridges but the principles hold true for shotgun and pistol as well.
Remember Fr. Frog's Rules of External Ballistics:
1) There ain't no magic bullets! (Although some are better than others for a particular purpose.)
2) Divide the range at which someone claims to have shot their deer by 4 to get the real range.
3) Always get as close as possible.
4) Don't believe manufacturer's claims.
5) Velocity erodes, mass doesn't
6) In the battle between velocity and accuracy, accuracy always wins.
7) Inconsequential increments are meaningless.
8) Most gun writers are pathological liars.
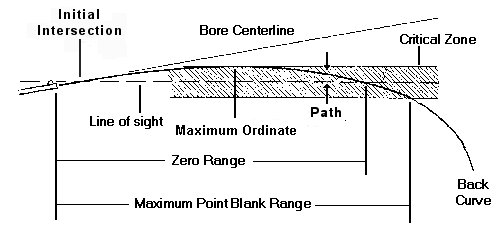
Many people believe that bullets fly in a straight line. This is untrue. They actually travel in a parabolic trajectory or one that becomes more and more curved as range increases and velocity drops off. The bullet actually starts to drop when it leaves the firearm's muzzle. However, the centerline of the bore is angled slightly upward in relation to the line of the sights (which are above the bore) so that the projectile crosses the line of sight on its way up (usually around 25 yards or so) and again on its way down at what is called the zero range.
Terms relating to external ballistics include:
Back Curve - This is that portion of the bullets trajectory that drops below the critical zone beyond the point blank range. Past this point the trajectory begins to drop off very rapidly with range and the point of impact becomes very difficult to estimate.
Ballistic Coefficient - This is a number that relates to the effect of air drag on the bullet's flight and which can be used to predict a bullet's trajectory under different circumstances through what are called "drag models." Technically a drag models applies only to a particular bullet, so using them to predict another bullet's performance is an approximation--but the results can be very close if the proper drag model is used. The most commonly used drag model is the G1 model (sometimes referred to--not really correctly--as C1) which is based on a flat-based blunt pointed bullet. The "standard" bullet used for this model has a ballistic coefficient of 1.0. A bullet that retains its velocity only half as well as the model has a ballistic coefficient of .5. The G1 model provides results close enough to the actual performance of most commercial bullets at moderate ranges (under about 500 yards) that it is commonly used for all commercial ballistics computation.
Note that there are two "standard" sets of meteorological conditions in common use. conditions" refer to an assumed used to standardize computations. The older one, is known as "Standard Metro" or "Army Standard" and the more modern "standard" is called the International Civil Aviation Organization (ICAO) standard. The characteristics of these two "standards" are listed below.
| Standard Metro | ICAO | |
| Altitude | Sea level (0') | Sea level (0') |
| Temperature | 59° F | 59° F |
| Barometric pressure | 29.5275" Hg | 29.9213" Hg |
| Humidity | 78% | 0% |
While they are similar, the different parameters do have a slight affect on calculations and in effect change the standard atmospheric density by about 1.8 percent. Under ICAO conditions the speed of sound 1116.5 f/s and under Standard Metro conditions it is 1120.27 f/s.
Since a quoted ballistic coefficient depends on atmospheric density, the same bullet has two different BCs depending on the conditions used. If a quoted BC based upon the "Standard Metro" conditions is used in a ballistics program based upon the ICAO standard the BC needs to be modified by multiplying it by .982. Conversely, ICAO based BCs need to be multiplied by 1.018. While this is a very small change and has little effect at short (under 600 yards) range it does have an effect at long ranges. The table below gives what various manufacturers use.
|
Mfgs BC Basis |
|
| Berger | ICAO |
| Barnes | Std Metro |
| Hornady | Std Metro |
| Nosler | ICAO |
| Remington | No Info received. Probably ICAO |
| Speer | They don't know. They use "local conditions" |
| Sierra | Std Metro |
| Woodleigh | No Info received. Probably Std Metro |
| Winchester | Std Metro |
A word to the wise. Many manufacturer give rather generous BCs for their bullets because: a) they want to look good--high BCs sell bullets; b) they were derived by visual shape comparison rather than actual firing data; or c) they were derived from short range firings rather than long range firings (which are more difficult to do). You should confirm your calculations by actual firing if you require exact data. Several manufactures have recently "readjusted" some of their BCs to more closely conform to actual firing data. For a more in-depth discussion of ballistic coefficients see the section below.
For a listing of BCs in Excel spreadsheet format, click here
Bore Centerline (Line of the bore)- This is the visual line of the center of the bore. Since sights are mounted above the bore's centerline and since the bullet begins to drop when it leaves the muzzle the bore must be angled upwards in relation to the line of sight so that the bullet will strike where the sights point.
Bullet Trajectory - This is the bullet's path as it travels down range. It is parabolic in shape and because the line of the bore is below the line of sight at the muzzle and angled upward, the bullet's path crosses the line of sight at two locations.
Critical Zone - This is the area of the bullet's path where it neither rises nor falls greater than the dimension specified. Most shooters set this as ± 3" to 4" from the line of sight, although other dimensions are sometimes used. The measurement is usually based on one-half of the vital zone of the usual target. Typical vital zones diameters are often given as: 3" to 4" for small game, and 6" to 8" for big game and (Gasp!) anti-personnel use.
Drag Model - A mathematical representation of the velocity decay of a projectile of a specific shape. Note that the decay is non-linear. Now coming into use are "drg" files the describe the bullet's drag at different velocities and which allow ballistic computations that don't need a BC and that use only simple math. The down side is that they require a specific "drg" file for each bullet and the data in the file must generally be determined on a Doppler radar range, although a close approximation can be computed by analysis of the bullet's dimensions.
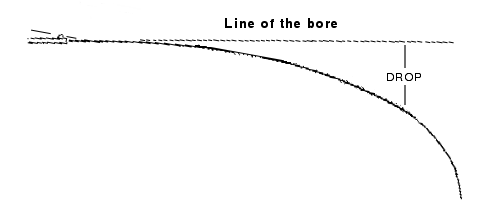
Drop - The distance a bullet falls below the line of the bore (at 90 deg to the line of the bore) when the bore is horizontal. Frequently mis-used to mean the bullet path in relation to the line of sight.
Initial Intersection - The range at which the bullet's trajectory first crosses the line of sight. This is normally occurs at a range of about 25 yards. Sometimes referred to a "near zero."
Line of Sight - This is the visual line of the aligned sight path. Since sights are mounted above the bore's centerline and since the bullet begins to drop when it leaves the muzzle the bore must be angled upwards in relation to the line of sight so that the bullet will strike where the sights point.
Maximum Ordinate - This is the maximum height of the projectile's path above the line of sight for a given point of impact and occurs somewhat past the halfway point to the zero range and it is determined by your zeroing range.
Maximum Point Blank Range - This is the farthest distance at which the bullet's path stays within the critical zone. In other words the maximum range at which you don't have to adjust your point of aim to hit the target's vital zone. Unless there is some over riding reason to the contrary shots should not generally be attempted much past this distance. In the words of the Guru, "It is unethical to attempt to take game beyond 300 meters." If you do, you should write yourself a letter explaining why it was necessary to do so. An approximate rule of thumb says that the maximum point blank range is approximately your zero range plus 40 yards.
Mid-range Trajectory - This is the height of the bullets path above the line of sight at half way to the zero range. It does not occur at the same range as the maximum ordinate height which can be greater.
Minute of Angle (MOA) - A "minute" of angle is 1/60 of a degree which for all practical purposes equates to 1 inch per 100 yards of range. (Actually it's 1.044") Thus 1 MOA at 100 yards is 1 inch and at 300 yards it is 3 inches. The term is commonly used to express the accuracy potential of a firearm.
Path - The distance a bullet's trajectory is above or below the line of sight.
Zero Range - This is the farthest distance at which the line of sight and the bullet's path intersect.
 |
|
Components of the
bullet's flight (path) |
 |
|
Drop |
A Brief Discourse on Ballistic Coefficients
This is probably the best article I have read on ballistic coefficients. It was written by Jim Ristow of Recreational Software, Inc. and is reprinted here with his permission. It was designed to encourage a discussion about ballistic coefficients and to explain why good BCs are crucial to getting accurate results from ballistic software. The illustrations and tables were not part of the original article.
A Little History
In 1881 Krupp of Germany first accurately quantified the air drag influence on bullet
travel by test firing large flat-based blunt-nosed bullets. Within a few years Mayevski
had devised a mathematical model to forecast the trajectory of a bullet and then Ingalls
published his famous tables using Mayevski's formulas and the Krupp data. In those days
most bullet shapes were similar and airplanes or missiles did not exist. Ingalls defined
the Ballistic Coefficient (B.C.) of a bullet as it's ability to overcome air resistance in
flight indexed to Krupp's standard reference projectile. The work of Ingalls &
Mayevski has been refined many times but it is still the foundation of small arms exterior
ballistics including a reliance on BCs.
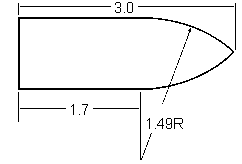 |
| The shape of the projectile used in the Krupp firings. It is 3 calibers long and has an ogival head with a 1.49 caliber radius. |
| Modern bullet designs. Much different than the Krupp bullet. Would you expect them to have the same drag characteristics? | |||
By the middle of the 20th century rifle bullets had become more aerodynamic and there were better ways to measure air drag. After WWII the U.S. Army's Ballistic Research Lab (BRL) conducted experiments at their facility in Aberdeen, MD to remeasure the drag caused by air resistance on different bullet shapes. They discovered air drag on bullets increases substantially more just above the speed of sound than previously understood and that different shapes had different velocity erosion due to air drag. In 1965 Winchester-Western published several bullet drag functions based on this early BRL research. The so-called "G" functions for various shapes included an improved Ingalls model, designated "G1". Even though the BRL had demonstrated modern bullets would not parallel the flight of the "G1" standard projectile, the "G1" drag model was adopted by the shooting industry and is still used to generate most trajectory data and B.C.'s. Amazingly, the "G1" standard projectile is close to the shape of the old blunt-nosed, flat-based Krupp artillery round of 1881!
The firearms industry has developed myriad ways to compensate for this problem. Most bullet manufacturers properly measure velocity erosion then publish B.C.'s using an "average" of the calculated G1 based B.C.'s for "normal" velocities. In other words, the only spot on the G1 curve where the model is correct is at the so-called "normal" or average velocity. These B.C.'s are off slightly at other velocities unless the bullet has the same shape, and therefore the same drag as the standard G1 projectile--few modern bullet do.
Some ballistic programs adjust the B.C. for velocities above the speed of sound, others use several B.C.'s at different velocities in an effort to correct the model. While these approaches mitigate some of the problem, B.C.'s based on G1 still cannot be correct unless the bullet is of the same shape as the standard projectile. Also, the change to air drag as a function of velocity does not happen abruptly. Drag change is continuous with only small variation immediately above or below any point along the trajectory. Programs that translate the Ingalls tables directly to computer or use multiple B.C.'s can produce velocity discontinuities when drag values change abruptly at pre-determined velocity zones. The resulting rapid changes to ballistic coefficient do not duplicate "real world" conditions. A BC based upon the correct drag model (which technically changes with every bullet) stays the same value. However, using a more modern drag model such as G7 the calculated ballistics comes closer to actuality than with the G1 and some manufacturers are beginning to supply G7 based BCs.
The Solution
Shooting software is finally appearing based on methods used in aerospace with drag models
for different bullet shapes. Results are superior to traditional "G1
fits everything" thinking, but now shooters must learn B.C.'s are different for each
model. Each bullet has a slightly different actual drag model and if the
exact drag model for a particular bullet is used the BC does not change with
changes in velocity. This could get cumbersome very fast with all the
bullets on the market.. However, most bullets actual drag models come
pretty close to matching one of the existing standard drag models as shown on
the graph below so we can get by with one of them and come much closer to
real life performance than with the catch-all G1/Ingalls. Note that if
the correct drag model is used (which technically is different for each bullet)
the BC does NOT change with velocity, and if a drag model is used that more
closely matches the actually drag model the BC will show less of a change at
different velocities than using a badly matched (G1) drag model.
This is a scary proposition for most bullet companies who know many shooters pick bullets based only on their B.C.'s. For example, A boat tailed bullet with a G1 based B.C. of .690 may actually have a G7 based B.C. of only .344, since the G7 drag model much more accurately describes its performance. But, everyone "knows" that .690 is "better" than .344. However, using the wrong drag model will yield trajectory data that indicates incorrect drop. Fortunately the differences only become important at very long range (>700 yards) but there is a difference. As an example the GI M80 Ball bullet (149 gr FMJ boat tail) has a verified G7 BC of .195. The commercial equivalents of this bullet are listed as having a G1 BC of between .393 and .395. You can see the differences in the plotted trajectories using both the G1 and G7 values and a program that handles both types.
| G1 = .393 | G7 = .195 | |||
|
Range |
Vel. |
Path |
Vel. |
Path |
|
0 |
2750 |
-1.5 |
2750 |
-1.5 |
|
100 |
2522 |
4.8 |
2520 |
4.9 |
|
200 |
2306 |
5.70 |
2302 |
5.7 |
|
300 |
2100 |
0.00 |
2094 |
0.00 |
|
400 |
1905 |
-13.6 |
1898 |
-13.7 |
|
500 |
1722 |
-36.8 |
1710 |
-37.0 |
|
600 |
1553 |
-71.8 |
1530 |
-72.3 |
|
700 |
1401 |
-121.3 |
1360 |
-122.6 |
|
800 |
1269 |
-188.4 |
1200 |
-191.7 |
|
900 |
1161 |
-277.2 |
1074 |
-285.1 |
|
1000 |
1078 |
-391.8 |
1014 |
-408.4 |
Modern ballistics uses the coefficient of drag (C.D.) and velocity (actually the bullet's Mach number rather than the traditional Ingalls/Mayevski/Sciacci s, t, a & i functions. This avoids velocity discontinuities and when combined with a proper drag model is far more accurate to distances beyond 1000 yards. A by-product of modern ballistics research is that the C.D. can be estimated fairly accurately from projectile dimensions and used to define custom drag models for unusual bullet shapes. (See caveat below.)
The drawing below shows how the various drag models vary.
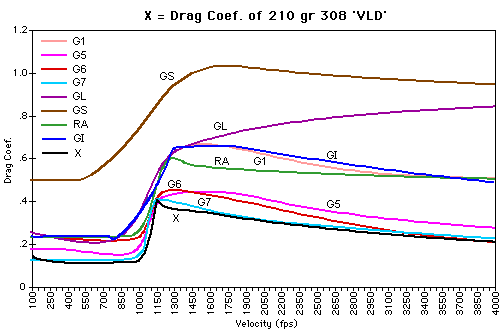
Note the difference between the G1 and the G5, G6, and G7!
The Coefficient of Drag for a bullet is simply an aerodynamic factor that relates velocity erosion due to air drag, air density, cross-sectional area, velocity, and mass. A simpler way to view C.D.'s are as the "generic indicator" of drag for any bullet of a particular shape. Sectional Density is then used to relate these "generic" drag coefficients to bullet size. The "Sectional Density" of a bullet is simply it's weight in pounds divided by it's diameter squared.
Sectional Density = (Wt. in Grains / 7,000) ÷ (Dia.* Dia).
You can see from the formula that a 1 inch diameter, 1 pound bullet (7,000 gr.) would produce a sectional density of 1. Indeed the standard projectile for all drag models can be viewed as weighing 1 pound and having a 1 inch diameter.
Another term occasionally found in load manuals is a bullet's "Form Factor". The form factor is simply the C.D. of a bullet divided by the C.D. of a pre-defined drag model's standard projectile.
Form Factor = (C.D. of any bullet) / (C.D. of the Defined 'G' Model Std. Bullet)
So What Is A Ballistic Coefficient?
Ballistic Coefficients are just the ratio of velocity retardation due to air drag (or
C.D.) for a particular bullet to that of its larger 'G' Model standard bullet. To relate
the size of the bullet to that of the standard projectile we simply divide the bullet's
sectional density by it's form factor.
Ballistic Coefficient = (Bullet Sectional Density) / (Bullet Form Factor)
From these short formulae it is evident that a bullet with the same shape as the 'G' standard bullet, weighing 1 lb. and 1 inch in diameter will have a B.C. of 1.000. If the bullet is the same shape, but is smaller, it will have an identical C.D., but a form factor of 1.000 and a B.C. equal to it's sectional density.
The following are the most common current drag models used in ballistics:
G1.1 - Standard model, flat based pointed bullet - 3.28 calibers in length, with a 1.32 caliber length nose, with a 2 caliber (blunt) nose ogive
G2.1 - Special model for a long conical point banded artillery projectile - 5.19 calibers long with a .5 caliber 6° boat tail. Not generally applicable to small arms.
G5.1 - For Moderate (low base) boat tails - 4.29 calibers long with a .49 caliber 7° 30' boat tail with 2.1 caliber nose with a 6.19 caliber tangent nose ogive
G6.1 - For flat based "spire point" type bullets - 4.81 calibers long with a 2.53 caliber nose and a 6.99 caliber secant nose ogive
G7.2 - For "VLD" type or pointed boat tails - 4.23 calibers long with with a .6 caliber long 7° 30' Tail Taper and a 2.18 caliber long nose with a 10 caliber tangent nose ogive. Most modern US military boat tailed bullets match this model.
G8.1 - Flat base with similar nose design to G7 - 3.64 calibers long with a 2.18 caliber long nose and a 10 caliber secant nose ogive. The US M2 152 gr .30 cal bullet matches this drag model. Close to the G6 model.
GS - For round ball - Based on 9/16" spherical projectiles as measured by the BRL. Larger and smaller sphere characteristics are effectively identical.
RA4 - For 22 Long Rifle, identical to G1 below 1400 f/s
GL - Traditional model used for blunt nosed exposed lead bullets, identical to G1 below 1400 f/s
GI - Converted from the original Ingalls tables. Essentially G1
GC - 3 caliber long flat nosed cylinder. Identical to G1 below 1200 f/s
To see what shapes these drag models are based upon, click here.
Nose Shapes
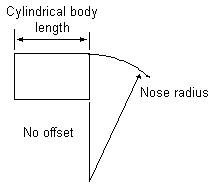
There are two basic types of nose shapes used on pointed bullets.
Tangent nose and secant nose. A
tangent nose shape has a radius the blends smoothly with the cylindrical portion
of the bullet's body, that is the radius used has its center point on a line
that is tangent to (at right angle to) the start of the cylindrical body.
With a secant nose shape the center point of the radius of the nose is offset
some distance from the start of the cylindrical body. Secant nose shapes
are ballistically more efficient but can cause issues with bullet seating depth
and standoff from the barrel's lands. The are also some "hybrid"
designs that combine both secant and tangent radii.
 |
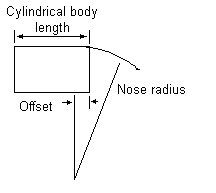 |
| Tangent Nose Radius | Secant Nose Radius |
For Best Accuracy, Calculate Your Own Coefficients!
Accurate B.C.'s are crucial to getting good data from your exterior ballistics software. A
good ballistic program should be able to use two velocities and the distance between them
to calculate an exact ballistic coefficient for any of the common drag models.
While you should really simultaneously measure the velocities at the 2 points
you can do very good work by measuring a minimum of 5 shots at the near
and far ranges and average each group.
This method of calculating a B.C. is preferred for personal use and can be used to duplicate published velocity tables for a bullet when the coefficient is unknown or to more accurately model trajectories achieved from your own firearm. A lot has changed in shooting software. If your software is more than two years old, chances are it does not employ the latest modeling techniques or calculate B.C.'s and even some of the newest software is not perfect as you can see from the next section.
If the industry wants to stay with a single BC drag model with modern bullets they would probably be better off using the G7 model than the G1. While not necessarily a perfect match the characteristic of modern bullets are much closer to the G7 drag model than the G1.
To order RSI's Shooting lab software you can go to www.shootingsoftware.com . Please tell him Fr. Frog sent you.

Effects Of Change In BC.
Small changes in BC value have very little effect until the ranges get past 5 - 600 yards.
| Range in Yards | Absolute Drop G7 BC = .195 |
Absolute Drop G7 BC = .200 |
| 100 | 2.44 | 2.43 |
| 200 | 10.4 | 10.3 |
| 400 | 47.3 | 47 |
| 600 | 123.7 | 122.1 |
| 800 | 260.5 | 255.8 |
| 1000 | 494.7 | 482.6 |
Bullet pictures courtesy Hornady Mfg.
Drag curves courtesy Jim Ristow
Some Caveats
We mentioned that CD can be estimated fairly well from certain bullet dimensions. However, because of the effects of bullet wobble (precession due to rotation), nose tip radius or flatness, nose curvature and boat tail, boundary layer interaction from cannelures and land engraving, etc. (all of which affect the wave drag, base drag and friction drag of the bullet differently) it is really impossible to predict with total accuracy the actual CD vs. Mach number. Also, while a ballistic coefficient can be computed from velocity measurements at two points, differences in bullet wobble diminishes the validity of chronograph testing for BC change over separate series of different muzzle velocities--it needs to be done by separate measurements at different ranges for each shot. Why? Read on.
An elongated bullet, as opposed to a round ball, is inherently unstable aerodynamically. When made stable gyroscopically by spinning, its center-of-gravity will follow the flight path. However, the nose of the bullet stays above the flight path ever so little just because the bullet has a finite length and generates some lift. This causes the bullet to fly at a very small angle of attack with respect to the flight path. The angle of attack produces a small upward cross flow over the nose that results in a small lift force. The lift force normally would cause the nose to rise and the bullet to tumble as the nose rose even more. That is where the spin comes in and causes the rising nose to precess about the bullet axis. When the spin is close to being right for the bullet's length, the precessing is minimized and the bullet "goes to sleep" If it is too slow the bullet will not be as stable as it should. (That is why Jeff Cooper says it's wrong to shoot groups at 100 yards for accuracy testing and suggests 300 yards. If your twist isn't right for the bullet used your group size will be larger at long ranges than would be expected by extrapolation of 100 yard data due to bullet wobble.) VLD (very low drag) bullets are very susceptible to precession and don't show their best accuracy until the get to 2-300 yards.
Of course, any other disturbing force such as a side wind gust could cause a difference in bullet nose precession but the effect would be quite small for a properly spin stabilized bullet. Most of the lift force is on the nose of the bullet and is proportional to the square of the bullet velocity as well as the nose shape and length. The new long-nosed bullets for long range match shooting can generate quite a bit more lift occurring farther ahead of the center- of-gravity and can produce a nasty pitch-up moment. That is why they require a faster than normal twist to stabilize them. Pistol bullets, being relatively short and with little taper to the nose, require a slower spin for stability.
Let's look at the rotational speed of a bullet. The formula for computing the rotational speed of a bullet is
R = (12/T) * V
where
T = Twist
V = Velocity in f/s
R = Rotations per second
R * 60 = Rotations per minute
Now consider a bullet chronographed at about 2750 f/s muzzle velocity fired from a rifle with a 10" twist. It is rotating at around 198,000 rpm Let the flight velocity decay to 2000 f/s. Now what is the bullet rotational speed? Well, it doesn't fall off much because the only things slowing it down are inertia and skin friction drag which is pretty low, and with the M80 ball bullet it has been measured about 90 percent of the original rpm (or in this case about 178,00 rpm) depending on the bullet. Then chronograph an identical bullet from the same rifle, this time with a muzzle velocity of 2000 f/s. Its rotational velocity will be 144,000 rpm. Its stability will be different from the bullet fired at 3000 f/s and allowed to slow down to 2000 f/s. It will not have the same drag at 2000 f/s although the bullets are identical. Therefore, two identical bullets fired from the same rifle at different velocities, will not have the same drag coefficient or ballistic coefficient just because of the way the measurements were taken. There are times when test data does not mean what you think it does. Again, radar range testing is the only way to fly for trustworthy bullet drag data. [I am indebted to Lew Kenner for this lucid description of bullet stability.]
Below is the rotational decay characteristic of the M80 Ball bullet which is typical.
| Range | Muzzle | 100 | 200 | 300 | 400 | 500 | 1000 |
|
Percent of spin remaining |
100 | 98 | 96 | 93 | 91 | 89 | 75 |
| Bullet RPM | 198,000 | 194,000 | 190,000 | 184,000 | 180,000 | 176,000 | 148,500 |
Another factor is that it is not necessarily true that the drag coefficient of a particular bullet is proportional to that of another bullet of the same design across the Mach number range, but this is what a ballistic coefficient assumes.
Something else to worry about is the effect of the bullet tip shape/condition on the ballistic coefficient. Because modern bullet have soft points they are subject to damage and manufacturing tolerances that can alter the BC from bullet to bullet and across otherwise similar bullets, although this affect is small unless there is a great deal of deformation.
For truly accurate results, individual bullet characteristics need to be measured on Doppler radar ranges as is done by the military--much too expensive a procedure for the commercial bullet industry who doesn't really care about great accuracy in BC calculations--and the drag model from those measurements applied only to the particular bullet tested. (If you have a spare $100,000 + and would like to buy me such a setup, let me know.)
The good news is that for normal rifle ranges the drag coefficients and ballistic coefficients can work satisfactorily for most purposes--so let's proceed.
To email me click here
| Ballistics Main Page | Internal Ballistics Page | Terminal Ballistics Page | Zeroing Page |
| Rifle Power Page | Misc. Questions |
| Back to Fr. Frog's Home Page |
Disclaimer
As far as I know all the information presented above is correct and I have attempted to insure that it is. However, I am not responsible for any errors, omissions, or damages resulting from the use or misuse of this information, nor for you doing something stupid with it. (Don't you hate these disclaimers? So do I, but there are people out there who refuse to be responsible for their own actions and who will sue anybody to make a buck.)
Updated 2014-09-14